A Quick Introduction to
Engineering
Statics and Mechanics of Materials
For SCA Fencers
Barwn Llwyd Aldrydd
M.k.a. Lloyd B. Eldred, Ph.D.
Introduction
The purpose of this article is to explain the basic theory and terminology used for engineering analysis of solid structures. We’ll cover the basics of static analysis, stress, strain, buckling, and cantilever bending. The choice of topics is designed to introduce what is necessary to have a basic discussion about the physics of what happens to a metal fencing blade during use.
This article covers several semesters of undergraduate engineering courses in a few pages. So, obviously, we’ll be hitting just the high points and skipping most of the tedious detail. Please feel free to contact me (Lloyd@galtham.org) with questions, suggestions for clarification and improvements, or corrections.
This article does propose some scenarios where epee-bending direction may contribute to failure in extreme load cases, but does not attempt to quantify what constitutes an extreme load. A follow-up article with numerical and computer calculations to address this issue is in the works.
A note on nomenclature: This article is being written for publication on the web, leading to some limitations on the use of common engineering symbols. Vector quantities are often indicated by drawing an arrow over the variable, I’ll be indicating them as a bold letter instead. Greek letters will either be written in English, e.g. “pi”, or have their meaning substituted as in “stress” rather than “sigma”.
Static Analysis
The basis for most engineering structural analysis is static theory. Recalling Newton’s second law:
F = m a
We can see that if an object is not undergoing acceleration (i.e. is stationary or in steady motion), then the object’s acceleration vector
a = 0
And thus the net applied force on the object must also be zero:
F = 0
This does not mean that a stationary object has no forces on it, just that the forces are all balanced in such a way that they add up to zero. The technical term for this state is equilibrium.
Consider a five pound block sitting on a table. It is being
pulled downward with a gravity force of 5 lb. Why then, isn’t it moving?
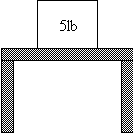
Figure 1: A block on a table
The answer is that the table is pushing up with a force that exactly cancels this gravity force, 5 lb. A free-body diagram (often abbreviated FBD) is a representation of the object in isolation with all other objects removed. All forces and moments (gravity, applied, and reactions applied by other objects) are indicated by arrows.
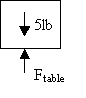
Figure 2: FBD of the block
If the vector F = 0, then the net forces in any direction must also sum to zero. So, if we sum up the vertical forces, taking a force pushing up as positive, and one pushing down as negative we get:
Ftable – 5 lb = 0
Algebra yields the obvious answer:
Ftable = 5 lb
(A quick aside: keeping your units with the numbers throughout a calculation is an excellent way to catch errors. If somehow we’d ended up with a force equal to 5 feet instead, we’d know there was an error somewhere in the calculation).
The next slightly more complex diagram represents an airplane in straight and level flight. It’s moving, but we can treat it as a static problem if it’s not changing speed, altitude, or attitude:
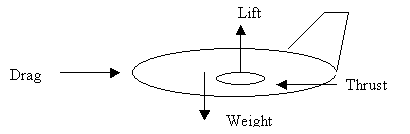
Figure 3: A very simple airplane in flight
Doing the same calculations as we did with the book example, but this time looking at both the horizontal and vertical directions, results in the following conclusions:
Thrust = Drag
Lift = Weight
The more alert reader will note that the aircraft pictured has a problem with unbalanced pitching moments (the way the weight and lift are illustrated, the aircraft will be pitching downward, and the drag and thrust indicated will produce a slight upward pitching moment). We’ll ignore that for now (a real aircraft will generally have a horizontal tail at the back of the aircraft that is providing a downward force to balance this moment).
Stress and Strain
Stress is a measure of the intensity of forces in an object. An engineer will compute the stress in an object and use this to predict deformation (how much the object stretches or compresses) and to check if the item is likely to fail (bend permanently or break). Stress is computed by dividing the applied force by the area of the object.
Stress = Force / Area
If the force is stretching the object, we describe the stress as “tensile” or “in tension”. If the force is crushing the object, we describe the stress as “compressive” or “in compression”. Stress has units of force over area, i.e. pounds per square inch (p.s.i.), or Newtons per square meter (also known as a Pascal).
Strain is a measure of the deformation of an object. It is measured by dividing the change in length by the original length. Thus, it can be considered to be unitless, but engineers will often write it as inches per inch just to keep in mind what the number represents.
Stress and strain are related. The higher the force, the more stress and the more deformation result. A tensile stress testing machine will produce a stress-strain diagram that looks something like:
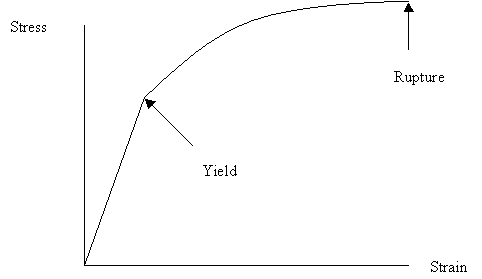
Figure 4: A typical Stress-Strain Plot
This plot shows a number of interesting features. There is a long linear region between zero stress/strain and the yield point of the material. In that region, we use Hooke’s Law to describe the relationship between stress and strain:
Stress = E strain
E is Young’s modulus or the modulus of elasticity. It’s the slope of the linear section of the stress-strain plot. The value of E varies from material to material and alloy to alloy and can be looked up in any engineering handbook. For generic steel, the most commonly used number is 30x106 psi, up to a yield stress of between 36 and 100 ksi (kilo pounds per square inch). Strain in this region of the curve is termed elastic, in that if the applied force is removed, the deformation returns to zero; the object is acting like a very stiff spring.
The curve then shows a long region of post yield strength. It has become slightly easier to stretch the object, but it hasn’t broken. Deformations in this part of the curve are termed plastic, in that part of the deflection is now permanent. If the applied force is removed, the object will only return some of the way to its initial shape. This portion of the curve can show some wiggles depending on if the material shows strain-hardening, or necking. The stress where the material breaks is called its ultimate strength and varies for steel alloys between 58 and 125 ksi.
Engineers generally design an object so that at maximum predicted load the maximum internal tensile load is still some factor of safety below the yield point
Columns
Next, lets consider a long column undergoing an axial compressive load:
![]()
Metal does not easily fail in compression, but another phenomena occurs: buckling. The bar becomes unstable and snaps into a curved shape. Try this on a straight epee or schlagger. The theory of stability is a complex one involving lots of calculus, but engineering handbooks list formulas for the buckling loads of different variations of this problem. The buckling load is the critical load after which it is possible for the column to snap out of being perfectly straight.
For this case, with one fixed end and one free end, the buckling load formula is:
Pcr = pi2 E I / (4 L2)
Where:
Pcr = critical (buckling) load
pi = 3.14159…
E = Elastic modulus of our material
I = Moment of inertia of the shape
L = column length
The Moment of Inertia is a measurement of how well the cross sectional shape resists bending. I-Beams are used in construction because their shape resists bending much better than a square beam made of the same amount of metal. Moments of Inertia for simple shapes can be looked up in an engineering handbook. Computing them for odd shapes (like an epee) requires calculus and is beyond the scope of this article. Further, as a fencing sword tapers from forte to tip, its moment of inertia decreases, so the above simple formula is no longer completely applicable.
Here, though are a couple of simple formulas that can use used to roughly approximate the moment of inertia for fencing swords.
Triangle: I = b h3 / 12
Where:
b = length of the base of the triangle
h = the height of the triangle
In the case of an epee, you could set b to an average value for the width of the “flat” part of the blade (side with the groove) and h to an average blade thickness.
Ellipse: I = pi a b3 /4
Where:
a = longer radius
b = shorter radius
You can also swap the two dimensions to get the moments of inertia that represent the bending stiffness in the other directions. Because of the cubed terms, those moments of inertia will be much higher! It is much harder to bend a fencing blade perpendicular to its natural direction.
A note of caution: the term “buckling” here should not be construed to mean “failed” or “broken”. The column still has substantial post-buckling strength and has not been damaged by this instability. Failure would require substantially larger deformations that would cause enough bending stress to reach the material yield point.
We curve our epees to pre-buckle them. Once bent, they no longer exhibit the very stiff rigid axial loading to a critical value followed by a snap out of line. Rather, they have a smooth, slowly increasing striking power.
Beam Bending
 This
brings us to another classic engineering structural problem: beam bending.
Consider a cantilever beam such as:
This
brings us to another classic engineering structural problem: beam bending.
Consider a cantilever beam such as:
When this beam is loaded with the downward tip force indicated, it will flex downward. When it flexes, the top portion of the beam will be stretching and thus under tensile stress and the bottom portion of the beam will be under compressive stress. At some point in the middle of the beam there will be a surface with zero stress – called the neutral axis.
Elastic beam theory says that for a beam with the same material properties throughout (not made of different metals, or having different parts of the beam undergoing different processes during manufacture) the neutral axis goes through the centroid of the cross section. The word “centroid” is a fancy word for center, meaning the axis where there is an equal area of material above and below the line.
Computing centroids is similar to computing moments of inertia. For complex shapes it requires calculus, but values for simple shapes can be looked up in any engineering handbook. Another perfectly accurate way to compute a centroid is to draw an enlarged version of the cross section on a stiff material such as cardboard. Cut out the cross section. Now balance the cut out on a ruler edge. When balanced, you have the same amount of material on either side of the ruler and the ruler edge is the neutral axis of that shape when bending is perpendicular to it.
So, where is the neutral axis for an epee? Good question! We probably need to do the cutout technique above to get an accurate measure. A solid triangle has a centroid that is one-third of the way from its base to the tip. A triangle with a half height triangle removed from its base (leaving a chevron shape) has its centroid at exactly half the way from the base to the tip. An epee is somewhere between these two shapes, so I’d assume the centroid is somewhere between one-third and one-half of the distance from the flat to the pointed side of the cross section. The location of the neutral axis may vary along the length of the blade depending on the relative depths of the various grooves.
The importance of the location of the centroid becomes clear when we look at the formula for the bending stress at any point in the cross section:
Bending stress = M y / I
Where:
M = bending moment
y = vertical distance from the neutral axis
I = moment of inertia of the cross section
M, the bending moment, is the vertical applied force multiplied by the distance from the tip.
Much more important for an epee, is the inclusion of “y” in this formula. If the centroid of the epee is closer to the flat than the pointed side, then the pointed side will see higher bending stresses than the flat side. The amount that they are higher may be as much as twice (if the centroid is at the one-third point) or as low as zero (if the centroid is in the middle). Don’t get ahead of me, though, higher bending stresses may or may not actually be a problem…
Combined Loading
A fencing sword hit is generally neither pure compression nor pure bending. We’re generally doing both, with most of the load on the blade being axial compression (“positive pressure in line with the blade”) and only a small portion of the load causing bending.
If we split the tip load into its axial and bending components we can add the two formulas to compute the stress at any point in the blade:
Stress = Paxial / Area + Pbending x y / I
Where
x = distance from the tip
y = distance from the neutral axis of the blade (positive on the inside of the bend, negative on the outside of the bend).
Note that both “x” and “I” increase as we move from the tip to the forte of the blade, so it’s not clear where along the blade the maximum stresses occur.
In most cases Paxial is much higher than Pbending. So, the entire blade will be in a net compressive load. It’s only when Pbending gets to be large that any of the blade will be under tension, and only when it’s very large that we’d get anywhere near the yield stress of the material. But, under those extreme cases failure is less likely if the region in tension is closer to the neutral axis. In other words, excessively bending an epee away from the flat may break slightly later than excessively bending it toward the flat. For a nominal maximum two-inch bend, it doesn’t even remotely matter.
Remember, surpassing the yield stress of a material causes plastic damage rather than breakage. It takes a much higher stress (150 to 200%) to cause rupture. This plastic damage is permanent. In other words: a kink in the blade. We do occasionally see blade kinks. The few broken blades that I’ve seen do not show much if any of this type of damage and they were not under unusual bending when they snapped. In those cases, there is another mechanism than bending causing the failure.
Quantifying the Stresses
If we do the cardboard cutout trick it may be possible to use these equations to do some back of the envelope estimations of the stresses in the blade. This should give us the right ballpark for the numbers involved.
In the next article in this series, I intend to do a somewhat better job and do a computer finite element analysis of an epee to compute the stresses in the blade under a variety of loads including typical combat loads and a FIE bending test load. I hope to be able to quantify the bending loads necessary to cause a failure in each direction (toward and away from the flat). The analyses are the easy part of this project. Producing a CAD model of an epee blade with reasonable dimensions and enough of the details to be representative of what we’re really using will take more time.
Other Issues
The theory discussed in this article and the finite element analyses to come are all linear elastic theory. They do not address issues such as fatigue and impact shock. Such issues are difficult to model and are way beyond the scope of this article.
The issue that struck my colleagues at work was the potential for crack inducement and other damage to the blade from parries. This seemed much more likely to be a significant source of blade breakage than the direction chosen for pre-buckling the blade.
References
Meriam, J.L., Kraige, L.G, “Engineering Mechanics, Volume 1, Statics,” Second Edition, John Wiley and Sons, 1986
Beer, F.P, Johnston, E.R. Jr., “Mechanics of Materials,” McGraw Hill 1981.